A simple guide to understanding math better through bar model drawing techniques

Wiki Article

Exploring Bar Model Drawing Techniques: A Comprehensive Guide to Imagining Math Concepts

Bar model attracting methods work as a beneficial source for both teachers and trainees in picturing mathematical ideas. These designs simplify intricate mathematical partnerships, assisting in the understanding of addition, subtraction, division, and reproduction. This overview details effective strategies for applying bar models, cultivating active involvement and real-world links. As visitors discover the useful applications and mentor ideas, they will certainly reveal how these methods can change their approach to mathematics.

Comprehending the Fundamentals of Bar Version Illustration

Bar version attracting functions as an effective aesthetic tool in mathematics, facilitating the understanding of analytic approaches and mathematical partnerships. This strategy entails representing numbers and their connections through rectangle-shaped bars, making it much easier to picture procedures such as enhancement, subtraction, division, and multiplication. Each bar's size matches to a specific worth, allowing students to contrast quantities and comprehend percentages plainly.

To create a bar version, one begins by identifying the issue's crucial elements, frequently simplifying right into parts that can be aesthetically represented. As an example, in a straightforward enhancement problem, 2 bars can be drawn, with their sizes representing the addends. The combined size shows the sum. Furthermore, bar designs can be adapted for more intricate troubles, consisting of portions and ratios, by adjusting benches accordingly. Grasping these fundamentals lays a strong structure for efficient analytical and much deeper mathematical comprehension.

Advantages of Making Use Of Bar Models in Mathematics

Using bar versions in maths offers countless benefits that boost discovering and comprehension. These aesthetic depictions aid trainees in comprehending complicated principles by breaking them down into convenient components. Bar designs give a clear framework for highlighting relationships in between numbers, making abstract concepts more concrete. They advertise a much deeper understanding of mathematical procedures and help with analytic by allowing learners to picture the data they are functioning with.

Moreover, bar versions support the growth of vital assuming skills, as trainees have to evaluate and translate the visual details to draw verdicts. This method urges energetic involvement with the material, reinforcing retention and proficiency of mathematical principles. By promoting a solid structure in visual literacy, bar versions equip students to come close to different mathematical difficulties with self-confidence. In general, the combination of bar designs into maths education and learning verifies helpful in growing both comprehension and analytical capacities amongst trainees.

Applying Bar Versions to Enhancement and Reduction

Bar models work as an effective device for visually standing for addition and subtraction problems. By highlighting the partnership in between numbers, they improve understanding and promote problem-solving. Additionally, real-life applications of these designs can aid students realize mathematical concepts in useful contexts.

Representing Enhancement Visually

When trainees run into addition and subtraction troubles, aesthetic aids can considerably improve their understanding of these procedures. Bar versions act as efficient tools for representing enhancement. By separating a rectangle right into sections that represent the numbers entailed, students can visualize the connection between the quantities. If a trainee needs to include 3 and 5, they can develop a bar separated into two sections: one section standing for 3 and the other representing 5. This clear depiction not just streamlines the enhancement procedure yet also reinforces the principle of incorporating quantities. As trainees manipulate these visual help, they develop a deeper comprehension of enhancement, bring about improved analytic skills and higher self-confidence in their mathematical capacities.

Subtraction With Bar Designs

Subtraction is frequently perceived as a more complex operation than enhancement, bar versions can efficiently clarify this process for trainees. By visually standing for the amounts included, pupils can much better understand just how numbers relate to one an additional. In a bar version for subtraction, one bar represents the total amount, while another suggests the quantity being subtracted. This visual distinction helps trainees comprehend the idea of "removing." As an example, if a bar shows 10 units, and another bar representing 4 systems is gotten rid of, students can easily see that 6 units continue to be. This method not only fosters understanding of subtraction but additionally help in establishing problem-solving abilities, enabling pupils to imagine their mathematical reasoning and enhance their total comprehension of mathematical principles.

Real-Life Application Instances

Understanding reduction through bar models lays a foundation for using these methods in real-life circumstances. In various contexts, such as budgeting or purchasing, individuals can envision exactly how much cash continues to be after costs. As an example, if an individual has $50 and invests $20, a bar design can stand for the total quantity and the invested portion, illustrating that $30 is left. Furthermore, moms and dads can make use of bar designs to help kids comprehend how many even more products need to be contributed to complete a set, such as having 3 apples and needing 5. This graph streamlines complex troubles, facilitating understanding and retention. Ultimately, bar models offer as effective devices in daily decision-making, enhancing mathematical understanding in practical situations.

Picturing Multiplication and Department With Bar Models

In exploring the application of bar designs for reproduction and department, it is important to comprehend their foundational principles. Building multiplication versions allows learners to picture relationships between numbers, while effective division techniques can be shown via these aesthetic help. This approach improves understanding and analytic abilities in mathematics.

Comprehending Bar Designs

Bar designs act as a powerful visual tool for highlighting the concepts of multiplication and division. They allow students to stand for mathematical relationships in an organized format, helping with a much deeper understanding of these procedures. In multiplication, bar designs display groups of equal dimension, permitting people to envision the overall amount when integrating these groups. Conversely, in department, bar models help illustrate exactly how a total is divided into smaller sized, equivalent components, making clear the principle of partitioning. By employing these aesthetic help, students can grasp the underlying principles of multiplication and division much more successfully. This approach not only enhances comprehension however likewise sustains analytic skills, making bar versions a very useful property in mathematical education and learning.

Creating Reproduction Designs

Building reproduction designs using bar layouts uses a clear method for visualizing the procedure of multiplication. These versions enable students to represent reproduction as teams of equal components, making abstract ideas much more concrete. As an example, to highlight (3 times 4), a trainee can attract one bar split into 3 equivalent sectors, each standing for four units. Furthermore, producing a second bar with the very same length enhances the understanding of repeated enhancement, as each section represents one team. This visual depiction not just aids in grasping reproduction but likewise improves problem-solving abilities. By using bar designs, trainees can much better comprehend partnerships between numbers and establish a durable foundation for more complex mathematical principles, leading to boosted self-confidence in their capabilities.

Envisioning Department Approaches

While reproduction often obtains the spotlight in early math education and learning, division is similarly necessary and can be efficiently imagined utilizing bar designs. Bar designs offer a clear visual representation of division troubles, damaging down the procedure right into workable parts. As an example, when splitting a total right into equivalent groups, trainees can draw a long bar to represent the whole and after that segment it into smaller bars that show each team. This method not just illustrates the principle of equal sharing but additionally reinforces the relationship in between reproduction and department. By utilizing bar models, students can better comprehend division as a process of partitioning, assisting to solidify their understanding of this fundamental mathematical operation.

Resolving Word Troubles Making Use Of Bar Version Techniques

Exactly how can graphes boost the understanding of word troubles? Bar version methods offer a powerful device for trainees to damage down complex situations right into manageable components. By translating words right into visual bars, learners can recognize relationships between amounts and operations more easily. Each bar represents a certain value, enabling trainees to see just how various components of the problem communicate.

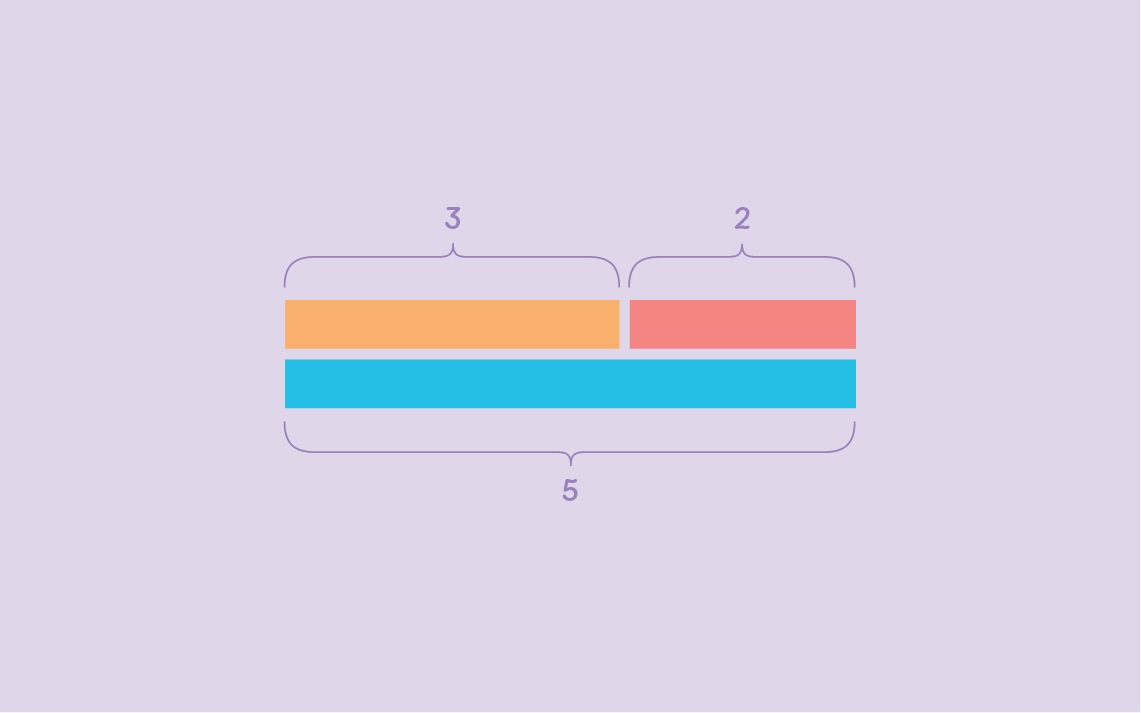
For instance, in a problem including addition and reduction, trainees can attract separate bars for each quantity and after that adjust them to discover the option. This process not only clears up the problem but also promotes a deeper conceptual understanding. Bar models can be adjusted for various kinds of word troubles, making them versatile throughout different mathematical topics. Inevitably, using bar models can significantly improve students' problem-solving skills by giving a clear visual pathway to reach the right solution.

Integrating Bar Models in Different Math Topics

Bar designs can be seamlessly integrated into various mathematics subjects, boosting pupils' understanding of concepts beyond basic arithmetic. In algebra, these aesthetic devices help in representing formulas and inequalities, enabling students to imagine relationships in between variables. When dealing with geometry, bar models can highlight the buildings of shapes and spatial thinking, aiding trainees realize concepts like area and boundary properly. In stats, bar designs promote the analysis of information sets, enabling students to contrast amounts and recognize trends aesthetically. Additionally, incorporating bar designs within measurement subjects help in understanding devices and conversions by offering a substantial representation of quantities. By employing bar models across different mathematical areas, educators can foster a deeper understanding of complicated principles, therefore enhancing analytical skills and promoting vital thinking (bar model drawing techniques). This convenience demonstrates the energy of bar designs as a foundational device for students in their mathematical trip

Tips for Teaching Bar Designs Efficiently

Incorporating bar designs bar model drawing techniques into teaching methods calls for thoughtful approaches to maximize their effectiveness. Educators ought to start by introducing bar models with easy, relatable instances that trainees can conveniently understand. This assists to build self-confidence and knowledge with the principle. Progressively boosting the complexity of problems permits students to use their abilities considerably. Additionally, teachers ought to motivate pupils to develop their very own bar versions, advertising energetic involvement and possession of their discovering.


Incorporating collaborative activities can additionally enhance understanding, as students discuss and fix troubles in teams. Continual responses is necessary; instructors need to give useful commentary on students' bar model representations to direct renovation. Ultimately, attaching bar models to real-life circumstances strengthens their importance, aiding pupils see the useful applications of their mathematical abilities. By executing these techniques, instructors can properly harness the power of bar versions in their maths direction.

Often Asked Concerns

Can Prevent Versions Be Made Use Of in Various Other Subjects Besides Mathematics?

Bar models can without a doubt be used in numerous subjects beyond mathematics. They efficiently illustrate ideas in science, social researches, and language arts, assisting to aesthetically represent connections, processes, and concepts for enhanced understanding across techniques.

What Age Is Ideal Fit for Understanding Bar Designs?

Bar designs are best matched for youngsters ages 7 to 12, as they establish concrete thinking abilities throughout this duration (bar model drawing techniques). At this age, pupils can properly understand abstract concepts via graph and analytic strategies

Exist Digital Equipment for Creating Bar Versions?

Yes, various digital devices exist for developing bar models, consisting of academic software program and online platforms. These devices help students picture mathematical ideas successfully, boosting their understanding and interaction in finding out with vibrant and interactive depictions.

Exactly How Can I Examine Pupil Recognizing of Bar Versions?

Examining student understanding of bar versions can include tests, empirical assessments, and team conversations. Educators may likewise examine trainees' completed versions and their capability to clarify their reasoning, guaranteeing an extensive examination of comprehension.

What Prevail Mistakes When Making Use Of Bar Designs?

Typical errors when using bar versions consist of misstating quantities, stopping working to precisely label bars, puzzling enhancement and subtraction, disregarding to use constant scales, and ignoring the significance of clear aesthetic separation in between various aspects.

In enhancement, bar versions can be adapted for much more complex issues, consisting of portions and ratios, by changing the bars appropriately. Reduction is typically perceived as an extra complicated operation than addition, bar versions can successfully clarify this process for students. In a bar model for subtraction, one bar stands for the total amount, while another indicates the quantity being deducted. If a bar shows 10 systems, and one more bar standing for 4 systems is removed, students can conveniently see that 6 units remain. When dividing a total amount right into equal groups, pupils can attract a long bar to represent the whole and after that section it right into smaller bars that show each team.

Report this wiki page